Johannes Carmesin

Prof Johannes Carmesin


Faculty for Mathematics and Computer Science
TU Freiberg
Prüferstraße 1, 09599 Freiberg, Germany


Room 1.07, Universitätshauptgebäude
E-Mail: Johannes.Carmesin@math.tu-freiberg.de
CV
Johannes Carmesin
Our group in Discrete Structures at TU Freiberg works on a broad range of topics in Graph Theory and related areas including Topology and Theoretical Computer Science.
European Prize in Combinatorics

Research team:


Dr Jan Kurkofka
Will J. Turner
Tim Planken
Joseph Devine


Recent interns: Romain Bourneuf (2023), Georgios Kontogeorgiou (2022), Lyuben Lichev (2019)

Secretary: Frau Caterina Löschner
Past members
Research seminar in Discrete Mathematics and Algebra (DMA)

Our research interests include:

Combinatorics in 3 dimensions

A key goal here is to extend the fundamental methods from Structural Graph Theory to study 2-dimensional simplicial complexes. The starting point for this project is my 3-dimensional analogue of Kuratowski's theorem.

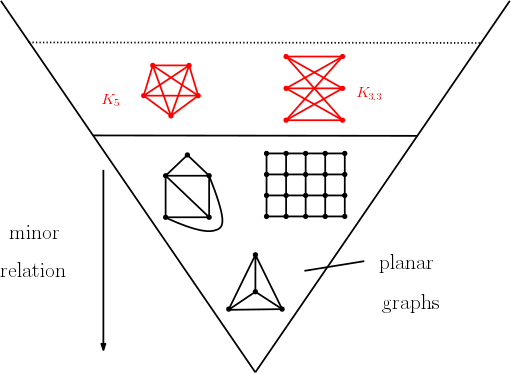
Graph Minors and Connectivity

A minor of a graph is obtained by deleting and contracting edges. The connection of Graph Minor Theory with topology is already apparent from this definition as deletions and contractions are "dual operations" for plane graphs, and even more so in the Graph Minor Structure Theorem of Robertson and Seymour . Here I am particularly interested in studying connectivity and tree-decompositions, and using its methods in other areas. New approaches include "local separators" of graphs as well as "angry theorems" for 3-connected graphs.

Matroids

A fundamental theorem in Matroid Theory is Whitney's characterisation of graph planarity in terms of matroids. I extended this theorem to 3-dimensional space. Another direction of research is to extend Whitney's theorem to surfaces, which led to a characterisation of graphs admitting locally planar embeddings.

Infinite Graphs

An important tool to study infinite graphs are ends, which can be seen as boundary points at infinity of the graph. In my PhD, I proved Halin's end-faithful spanning-tree conjecture in amended form. A big problem in the area is whether countable graphs are well-quasi ordered (this implies an abundance of well-quasi ordering conjectures in finite graph theory as well).

Selected Papers

  1. Local 2-separators, Journal of Combinatorial Theory, Series B, Volume 156, 2022, Pages 101-144, pdf
  2. Canonical decompositions of 3-connected graphs (with J. Kurkofka), FOCS 2023, 50 pages; pdf
  3. Embedding simply connected 2-complexes in 3-space, pages 91, Preprint; pdf
  4. All graphs have tree-decompositions displaying their topological ends, Combinatorica, Volume 39 (2019), pages 545-596; pdf
  5. Graph Theory - A Survey on the Occasion of the Abel Prize for László Lovász, Jahresbericht der Deutschen Mathematiker-Vereinigung volume 124, pages 83-108 (2022); pdf
Click here to see the recent papers of our group.
Click here to see all my papers.

Recent papers of our group

Preprints

2024

2023

2022

Editorships

Innovations in Graph Theory
Discrete Mathematics

Papers

  1. Towards a Stallings-type theorem for finite groups (with G. Kontogeorgiou, J. Kurkofka, W. Turner), Preprint; pdf
  2. How to apply tree decomposition ideas in large networks? (with S. Frenkel), Preprint; pdf
  3. Embedding simply connected 2-complexes in 3-space, Preprint; pdf
  4. Canonical decompositions of 3-connected graphs (with J.Kurkofka), FOCS 2023, 50 pages; pdf
  5. Characterising 4-tangles through a connectivity property (with J.Kurkofka), Preprint; pdf
  6. Graph Theory - A Survey on the Occasion of the Abel Prize for László Lovász, Jahresbericht der Deutschen Mathematiker-Vereinigung volume 124, pages 83-108 (2022); pdf
  7. Dual matroids of 2-complexes -- revisited, Preprint; pdf
  8. On Andreae's Ubiquity Conjecture, Journal of Combinatorial Theory, Series B 162, pages 68-70 (2023); pdf
  9. Entanglements (with J. Kurkofka), Journal of Combinatorial Theory, Series B 164, pages 17-28 (2024); pdf
  10. A characterisation of 3-colourable 3-dimensional triangulations (with E. Nevinson and B. Saunders), Preprint; pdf
  11. Outerspatial 2-complexes: Extending the class of outerplanar graphs to three dimensions (with T. Mihaylov), Preprint; pdf
  12. A Whitney type theorem for surfaces: characterising graphs with locally planar embeddings, Preprint; pdf
  13. Characterising graphs with no subdivision of a wheel of bounded diameter, Journal of Combinatorial Theory, Series B, Volume 161, Pages 21-51 (2023); pdf
  14. Local 2-separators, Journal of Combinatorial Theory, Series B, Volume 156, 2022, Pages 101-144, pdf
  15. Large highly connected subgraphs in graphs with linear average degree, Preprint; pdf
  16. New Constructions related to the Polynomial Sphere Recognition Problem (with L. Lichev), Discret. Comput. Geom., volume 67, 2022, pages 1097-1123; pdf
  17. Canonical trees of tree-decompositions (with M. Hamann and B. Miraftab), Journal of Combinatorial Theory, Series B, Volume 152, 2022, Pages 1-26; pdf
  18. The Almost Intersection Property for Pairs of Matroids on Common Groundset (with N. Bowler, S. Ghaderi and J. Wojciechowski), The Electronic Journal of Combinatorics, Pages 3-5 (2020); pdf
  19. Embedding simply connected 2-complexes in 3-space I, Preprint; pdf
  20. Embedding simply connected 2-complexes in 3-space II, Preprint; pdf
  21. Embedding simply connected 2-complexes in 3-space III, Preprint; pdf
  22. Embedding simply connected 2-complexes in 3-space IV, Preprint; pdf
  23. Embedding simply connected 2-complexes in 3-space V, Preprint; pdf
  24. On tree-decompositions of one-ended graphs (with F. Lehner & R. Möller), Math. Nachrichten 292.3: Pages 524-539 (2019); pdf
  25. A Liouville hyperbolic souvlaki (with B. Federici & A. Georgakopoulos), Electron. J. Probab., Volume 22 (2017), paper no. 36, 19 pages; pdf
  26. The colouring number of infinite graphs (with N. Bowler, P. Komjáth & C. Reiher), Combinatorica, Volume 39, Pages 1225-1235 (2019); pdf
  27. A short proof that every finite graph has a tree-decomposition displaying its tangles, European J. Combin. 58 (2016), 61-65; pdf
  28. Canonical tree-decompositions of a graph that display its k-blocks (with Pascal Gollin), J. Combin. Theory Ser. B , Volume 122 (2017), Pages 1-20; pdf
  29. Reconstruction of infinite matroids from their 3-connected minors (with N. Bowler & L. Postle), European J. Combin. (2018), volume 67, pages 126-144; pdf
  30. Every planar graph with the Liouville property is amenable (with Agelos Georgakopoulos), Random Structures & Algorithms 57.3: Pages 706-729 (2020); pdf
  31. All graphs have tree-decompositions displaying their topological ends, Combinatorica, Volume 39 (2019), pages 545-596; pdf
  32. Topological cycle matroids of infinite graphs, European J. Combin, Volume 60 (2017), Pages 135-150; pdf
  33. Infinite trees of matroids (with Nathan Bowler), Preprint; pdf
  34. On the intersection conjecture for infinite trees of matroids (with Nathan Bowler), Preprint; pdf
  35. Even an infinite bureaucracy eventually makes a decision, Preprint; pdf
  36. Topological infinite gammoids, and a new Menger-type theorem for infinite graphs, Electron. J. Combin. 25(2018), no. 3, paper 3.38, 22pp; pdf
  37. Infinite graphic matroids Part I (with Nathan Bowler & Robin Christian), Combinatorica (2018), volume 38, issue 2, pages 305-339; pdf
  38. Edge-disjoint double rays in infinite graphs: a Halin type result (with Nathan Bowler & Julian Pott), J. Combin. Theory Ser. B 111 (2015), 1-16; pdf
  39. The ubiquity of Psi-matroids (with Nathan Bowler), Preprint; pdf
  40. Infinite Matroids and Determinacy of Games (with Nathan Bowler), Preprint; pdf
  41. Canonical tree-decompositions of finite graphs II. Essential parts (with R. Diestel, M. Hamann & F. Hundertmark), J. Combin. Theory Ser. B 118 (2016), 268-283; pdf
  42. Canonical tree-decompositions of finite graphs I. Existence and algorithms (with R. Diestel, M. Hamann & F. Hundertmark), J. Combin. Theory Ser. B 116 (2016), 1-24; pdf
  43. k-Blocks: a connectivity invariant for graphs (with R. Diestel, M. Hamann & F. Hundertmark), SIAM J. Discrete Math. , 28-4 (2014), pp. 1876-1891; pdf
  44. An excluded minors method for infinite matroids (with Nathan Bowler), J. Combin. Theory Ser. B (2018), volume 128, pp. 104-113; pdf
  45. Matroid intersection, base packing and base covering for infinite matroids (with Nathan Bowler), Combinatorica 35 (2015), no. 2, 153-180; pdf
  46. Matroids with an infinite circuit-cocircuit intersection (with Nathan Bowler), J. Combin. Theory Ser. B (2014), volume 107, 78-91; pdf
  47. On the intersection of infinite matroids (with Elad Aigner-Horev & Jan-Oliver Fröhlich), Discrete Mathematics (2018), volume 341, issue 6, pages 1582-1596; pdf
  48. Connectivity and tree-structure in finite graphs (with Reinhard Diestel, Fabian Hundertmark & Maya Stein), Combinatorica 34 (2014) , 11-46; pdf
  49. A characterization of the locally finite networks admitting non-constant harmonic functions of finite energy, Potential Analysis 37 (2012), 229-245; pdf

Habilitation (2018)

Dissertation (2015)

Master thesis (2012)